Graphing Relations
There are two ways to think about drawing a picture of a relation on a set $A$.
if $A=\mathbb{R}$
We can draw relations on $\mathbb{R}$, because they are subsets of $\mathbb{R}\times\mathbb{R}$ — i.e., subsets of the plane. Actually you’ve been drawing these pictures since way back.
For example, let’s consider the relation $S$ given by $x\operatorname{S}y$ if $x^2-y^2\leq 1$. The picture looks like:
Here I’ve put $S$ in blue, and its complement $S^c$ in red.
What does $S^{-1}$ look like? $x\operatorname{S}^{-1}y$ means $y\operatorname{S}x$, i.e. $y^2-x^2\leq 1$. Here’s that, in green.
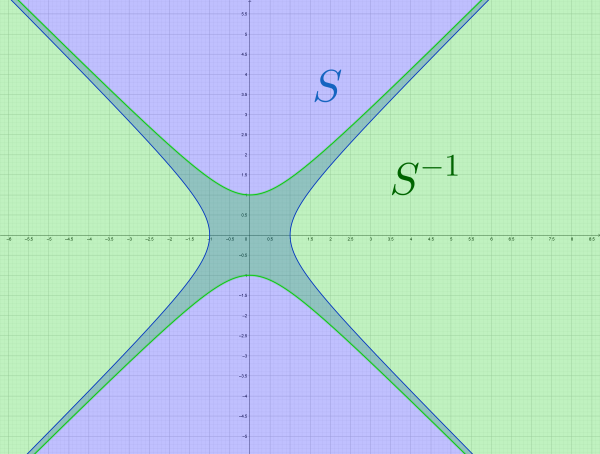
Notice that $S^{-1}$ and $S^c$ are general rather different things (that’s as we saw before).
To get $S^{-1}$ from $S$, we swap the roles of $x$ and $y$. visually, this looks like reflection across the line $y=x$. Here’s another example, with the line $y=x$ draw on explicitly:
We can use such a visual depiction to compute the domain and range of a relation: the domain is the “horizontal shadow” and the range is the “vertical shadow:
We can also use such a depiction to check some properties of relations. For example: for $R$ to be reflexive on $\mathbb{R}$ means every $x\in\mathbb{R}$ has $x\operatorname{R}x$. That is, every pair $(x,x)\in R$. All of the pairs of the form $(x,x)$ constitute the diagonal line $y=x$. Thus we can check reflexivity by asking: does the relation contain the diagonal line?
Here the relation $R$ is reflexive — it contains the line $y=x$ — and the relation $S$ is not.
We can also check symmetry. For $R$ to be symmetric means $x\operatorname{R}y$ guarantees $y\operatorname{R} x$. That is, if we reflect $R$ across the line $y=x$, we should land in in $R$ again. That is, $R$ being symmetric means $R$ is symmetric about the line $y=x$. Neither $R$ nor $S$ above is symmetric.
Transitivity is a bit more fun to check. Transitivity is relevant to pairs $(x,y)$ and $(y,z)$ both in $R$. Here we’ll check whether $S$, given by $x\operatorname{S}y$ if $x^2-y^2\leq 1$, is transitive. We have $.8\operatorname{S}.6$ and $.6\operatorname{S}.2$, so we check to see if $.8\operatorname{S}.2$. Here, $(.8,.2)$ is indicated in red — it’s in $S$. But we need this to hold for every such pair of points in $S$.
Unfortunately, it does not:
It’s a bit hard to see visually just what transitivity means, but you can see that it’s got something to do with right triangles.
if $A$ is a finite set
If $A$ is a finite set, we can draw what’s called a directed graph, or digraph, of the relation $R$. A directed graph is a collection of vertices, which we draw as points, and directed edges, which we draw as arrows between the points. For example, let’s take the set $A=\{2,3,4,5,6,7,8,9\}$ and the relation $(x,y)\in R$ if $x|y$.
The digraph corresponding to this relation is draw like this: we know $2|4$, $2|6$, and $2|8$. So we draw three arrows starting from 2. We also know that $3|6$ and $3|9$, so we draw those:
But that’s not all. We also know that $9|9$, for example. So we need to add arrows that start and end at each vertex:
Observe that divides, as a relation on this set, is transitive: whenever we have $x|y$ and $y|z$, we automatically have $x|z$. We can recognize this in the digraph by checking that, whenever there are two arrows connected head to tail, the third leg of that triangle is present:
Exercise. What do symmetry and reflexivity look like in the digraph?