Computational Methods
Computational Methods
We take part in theoretical methods development to study physical properties of condensed phases.
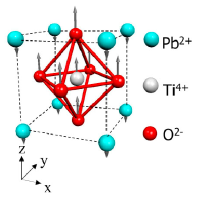
Recent Related Works
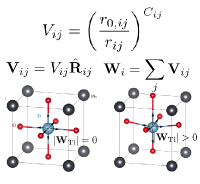
We developed a model potential based on the principles of bond-valence and bond-valence vector conservations for various perovskite-type oxides which then allows the quantitative, atomistic, multi-scale study of polarization switching, electric-field-driven domain wall motion and origin of relaxor behavior.
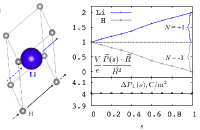
We developed quantum mechanically rigorous method that unambiguously partitions electrons among atoms in insulators that naturally gives rise to integer number oxidation states. The method employs Berry phase polarization change upon shifting a sublattice by a lattice vector and depends only on the topology of the wavefunction, therefore avoiding the probabilistic real space distribution of the charge density.

Dynamic pair distribution function (DPDF) is the probability of frequencies of oscillations at a give distance for atomic pairs. This technique can reveal vibrational modes in addition to favorable distance, obtained from the pair distribution function (PDF) widely used, for different types of atomic pairs in compounds. Computationally, we first calculate PDF advancing time delay; we called the PDF time delay PDF. Whenever time delay reaches time period of the motion for an atomic pair, a strong peak in time delay PDF appears at a favorable distance. The DPDF is Fourier transform of the time delay PDF from time domain into frequency domain. Thus, the peaks of the DPDF provide information of frequencies which correspond to vibrational mode and structures. The DPDF is quite useful for analysis of local sturcture nad dynamics especially for complex materials.
Related Publications
- H. Takenaka, I. Grinberg, and A. M. Rappe, “Anisotropic local correlations and dynamics in a relaxor ferroelectric”, Phys. Rev. Lett. 110, 147602 (1-5) (2013).PDF
- S. Liu, I. Grinberg, and A. M. Rappe, “Development of a bond-valence based interatomic potential for BiFeO3 for accurate molecular dynamics simulations”, J. Phys. Cond. Matt. 25, 102202 (1-6) (2013).
PDF - L. Jiang, S. V. Levchenko, and A. M. Rappe,
“Rigorous Definition of Oxidation States of Ions in Solids”,
Phys. Rev. Lett. 108, 166403 (1-5) (2012).
PDF
Supplementary material
PDF - T. Qi, Y.-H. Shin, K.-L. Yeh, K. A. Nelson, and A. M. Rappe,
“Collective Coherent Control: Synchronization of Polarization in
Ferroelectric PbTiO3 by Shaped THz Fields”, Phys. Rev. Lett.
102, 247603 (1-4) (2009).
PDF - Y.-H. Shin, B.-J. Lee, and A. M. Rappe,
“Bond-valence model of Ferroelectric PbTiO3“, J. Kor. Phys.
Soc. 52, 1206-10 (2008).
PDF - Y.-H. Shin, J.-Y. Son, B.-J. Lee, I. Grinberg, and
A. M. Rappe, “Order-disorder character of
PbTiO3“, J. Phys.: Cond. Matt. 20, 015224 (1-5) (2008).
PDF - Y.-H. Shin, I. Grinberg, I.-W. Chen, and A. M. Rappe,
“Nucleation and growth mechanism of ferroelectric domain-wall motion”,
Nature 449, 881-6 (2007).
PDF
Supplementary material
PDF - Y.-H. Shin, V. R. Cooper, I. Grinberg, and A. M. Rappe,
“Development of a bond-valence molecular-dynamics model for complex
oxides”, Phys. Rev. B 71, 054104 (1-4) (2005).
PDF
