Condensed Matter Physics
Condensed matter physics aims to understand the behaviors of solid and liquid materials. Practitioners employ a variety of theoretical tools, from quantum mechanics to statistical mechanics, and a variety of experimental tools, from scattering to spectroscopy. Over the years Yodh’s group has explored many problems in condensed matter physics. Some of this research is described in this web site.
Soft Materials & Complex Fluids
Soft condensed matter physics is concerned with materials such as colloidal suspensions, emulsions, polymer solutions, gels, membranes, liquid crystals and mixtures thereof, whose structure and dynamics are strongly influenced by entropy and by relatively weak mechanical forces. They provide a fascinating testing ground for investigation of fundamental questions in condensed matter physics, for example, many-body statistical physics, rheology, hydrodynamics, entropic forces and self-assembly, topological defects, melting, freezing, jamming and other instabilities. Research on these substances is technology driven too. Soft materials are attractive starting media in photonics and lithography, in high-tech ceramics and in biochemical sensing. Particle additives also offer practical control of fluid rheologies, improving the performances of materials ranging from conventional paints and pastes to motor oils to food and cosmetics. Recently, soft matter has grown to encompass a host of non-equilibrium problems and materials such as arise in the study of granular media and foams. Finally, complex fluids experiments are increasingly stimulated by analogies from cell biology, in some cases providing critical insights about mechanisms that arise in crowded cellular environments.
Coffee Ring Physics (and much more)
The phenomenon called the coffee-ring effect occurs when a drop of coffee dries. Briefly, as the drop evaporates, its’ edges become pinned and cannot recede towards the middle of a drop. As a result, fluid flows from the middle of the drop to the edge of the drop to replenish evaporated water. This flow carries suspended particles, moving them from the drop center to its edges, and thus producing a coffee-ring (after drying). Why should we care about this everyday effect? In fact, an evaporating colloidal drop is a complex, difficult-to-control, non-equilibrium system. To understand it, one must elucidate the consequences of interface pinning, fluid dynamics, particle-substrate interactions, substrate-fluid interactions, capillary interactions at the air-water interface, and more. These intellectual challenges motivated our experiments, but the insights gained can also influence practical applications in printing, genotyping, and in other complex assembly and coating schemes.
A Drying Drop of Ellipsoidal Particles Does Not Leave a Coffee Ring: We discovered that the shape of the colloidal particles suspended in the evaporating drop can affect the drying pattern. In particular, ellipsoidal-like particles deform the air-water interface, which in turn induces strong inter-particle capillary attractions between ellipsoids on the air-water interface. This capillary attraction prevents ellipsoids from getting to the drop edge, and it causes the ellipsoids to form a loosely packed but strongly bound network that can cover the entire air-water interface. The resultant effect is that the ellipsoids are left much more uniformly distributed on the underlying substrate surface when evaporation is complete. Thus, particle shape can prevent coffee-rings and help produce uniform coatings.
More Consequences of Shape-Dependent Capillary Interactions:
Following up on this surprising initial observation, we carried out other experiments with the ellipsoidal particles and uncovered other fascinating phenomena. For example, instead of sessile drops, we studied evaporation and deposition from drops confined between two walls. This research again revealed dramatically different behaviors between drops containing spheres compared to drops containing ellipsoids. The ultimate reason for these differences was again related to strong capillary interactions between particles residing on the air-water interface, but the detailed mechanisms that brought about the phenomena involve interface buckling and are therefore quite different for the confined drops compared to the sessile drops. Another set of experiments explored the deposition roughness and growth of particles at the drop edge in greater detail. We discovered that when we tuned the shape anisotropy of the ellipsoids, and thereby varied their lateral interactions, the roughness of the deposition growth profile changed. Interestingly, it exhibited growth behaviors characteristic of different universality classes, including the famous “KPZ” universality class.
More Coffee Ring Effects: Other studies explored different system. One set of investigations focused on the effects of surfactants on evaporating colloidal drops of spheres. The addition of surfactants, in some cases, created Marangoni eddies, among other effects, which led to differences in drying dynamics and deposition. Very recently, we explored drying of liquid crystal drops. These drops differ qualitatively from most others due to their concentration-dependent isotropic, nematic, and columnar liquid crystalline phases that form in water. As a result, although the lyotropic chromonic liquid crystal droplets start drying in the dilute isotropic liquid phase, as drying proceeds solute concentration increases and gradients develop and then ordered liquid crystal phases arise in different parts of the drop during evaporation. The concentration profiles, and the formation and separation of liquid crystal phases, in turn, create density, viscosity and surface tension effects that drive development of new convective currents, drop morphologies, and deposition patterns.

Liquid Crystal Physics
Liquid crystals are phases of matter that “fit” somewhere between traditional fluids and crystalline solids. Most liquid crystals flow and take the shape of the container that holds them. However, the molecules that comprise the liquid crystal are anisotropic (e.g., rod-like); in its nematic phase these molecules within tend to align along a single direction, defining the so-called nematic director, even when the liquid is not flowing. Nematic liquid crystals have internal orientational order but lack internal positional order. This feature, and others, endow liquid crystals with rich and fundamentally new properties. Furthermore, dynamic control of the alignment and realignment of the liquid crystal director underlies a multi-billion dollar display industry.
Chromonic Liquid Crystals: Lyotropic chromonic liquid crystals (LCLCs) are composed of organic, charged, plank-like molecules that self-assemble in water into columnar or rod-like aggregates. These aggregates, in turn, can self-assemble to form nematic, columnar and other phases in water. Importantly, in contrast to thermotropic LCs, i.e., the LCs used in display technology, chromonic liquid crystal mesogens are soluable in water and thus LCLCs offer new potential to integrate liquid crystal technology with biomaterials. In addition, far less is known about their fundamental science compared to the thermotropics.
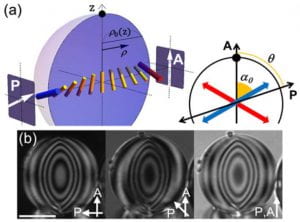
Our group has been investigating LCLCs in a variety of geometries, for example, within spherical drops, in hollow cylinders, and between parallel plates. We have also developed ways to alter the anchoring conditions of chromonic aggregates (rods) on the surfaces of these containers, e.g., with directors parallel or perpendicular to the containing walls. These studies enable us to probe the subtle interplay between bulk liquid crystal elasticity, container geometry, and defect topology which ultimately affects liquid crystal structure. One especially interesting feature derives from the fact that LCLC twist elasticity tends to be much weaker than its bend and splay elasticities; thus the liquid crystal director (internal orientation) readily twists, and the nematic phase can spontaneously form chiral structures. Thus, our work also sheds light on the origins of chiral symmetry breaking. In spherical drops, for example, we observed twisted bipolar structures of the nematic phase director with unusually large twist, and surprisingly we even observed facetted drops associated with the columnar phase (figure 1a-c). In cylinders with perpendicular (homeotropic) boundary conditions for the director, we discovered twisted-escaped-radial configurations of the LCLC, as well as new kinds of defects that separated structures with differing chirality and escape direction. In cylinders with parallel boundary conditions for the director, we measured a “fourth” type of elasticity called saddle-splay for the first time in LCLCs (figure 2).
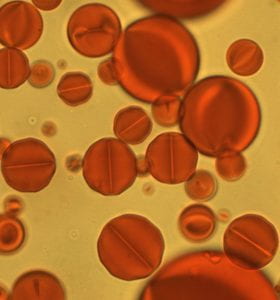
 Liquid Crystal Janus Drops (and more): Janus colloids have captured the interest of many soft matter scientists, some of whom study equilibrium properties and some of whom study non-equilibrium (active matter) phenomena. Janus colloids are composed of two-faced particles or droplets. Spatial anisotropy can arise from arrangements of patches on the particle/droplet surface, or from the placement of compartment volumes with distinct characteristics within the particle/droplet volume. Surprisingly, most Janus colloids explored to date utilize only isotropic materials. To this end, we prepared the first liquid crystal (LC) Janus droplets (figure) by combining microfluidics and phase separation techniques. We showed how an anisotropic LC component can introduce new functionalities into Janus droplets and how these properties lead to other unusual behaviors including swimming.
Liquid Crystal Janus Drops (and more): Janus colloids have captured the interest of many soft matter scientists, some of whom study equilibrium properties and some of whom study non-equilibrium (active matter) phenomena. Janus colloids are composed of two-faced particles or droplets. Spatial anisotropy can arise from arrangements of patches on the particle/droplet surface, or from the placement of compartment volumes with distinct characteristics within the particle/droplet volume. Surprisingly, most Janus colloids explored to date utilize only isotropic materials. To this end, we prepared the first liquid crystal (LC) Janus droplets (figure) by combining microfluidics and phase separation techniques. We showed how an anisotropic LC component can introduce new functionalities into Janus droplets and how these properties lead to other unusual behaviors including swimming.
See publications and other subsections to learn about our research on lyotropic liquid crystals based on fd-virus, the assembly of particles on liquid crystal surfaces, light diffusion and correlation transport transport through nematic liquid crystals, diffusion of biopolymers in liquid crystals, and more.
Solid-Solid Phase Transitions
Solid–solid (s–s) transitions between different crystalline structures are among the most numerous of nature’s phase transitions. These transformations are exhibited by elemental crystals, alloys and minerals, and they hold broad implications in earth science, diamond and steel production, and the synthesis of ceramic materials. Despite their considerable technological importance, however, the mechanisms that govern s–s phase transitions present substantial challenges for theory, simulation and experiment. A central question about the nature of s–s transitions, for example, concerns their kinetic pathways. Do these pathways follow a martensitic transformation with particles moving in concert or do they follow a diffusive nucleation process?
 Our experiments observed nucleation processes in the s–s transitions of colloidal crystals with single-particle resolution. This model thermodynamic system, based on temperature-sensitive colloids composed of micrometer-sized particles whose thermal motions can be directly visualized by video microscopy, has already provided many general insights about phase transitions, including the dynamics of crystallization, melting, sublimation, glass formation and jamming transitions (you can find other examples on this research page, in our publications, and elsewhere). In our experiment, high-quality large crystalline domains and a local heating technique enable us to study homogeneous nucleation and heterogeneous nucleation near defects. Notably, we discovered a surprising two-step nucleation behaviour during the s-s transformation between crystals with square and triangular lattices; during the process the system passed through an intermediate liquid stage (figure). This surprising phenomena can be expected to occur in crystals with constituents at any length scale, provided that solid–liquid interfacial energies are sufficiently small. Further, our single-particle experimental resolution enabled us to directly identify liquid nucleation precursors, which arise from particle-swapping loops rather than from defects, and to study the facets of evolving nuclei, whose energetics and growth rates exhibit rich phenomenology.
Our experiments observed nucleation processes in the s–s transitions of colloidal crystals with single-particle resolution. This model thermodynamic system, based on temperature-sensitive colloids composed of micrometer-sized particles whose thermal motions can be directly visualized by video microscopy, has already provided many general insights about phase transitions, including the dynamics of crystallization, melting, sublimation, glass formation and jamming transitions (you can find other examples on this research page, in our publications, and elsewhere). In our experiment, high-quality large crystalline domains and a local heating technique enable us to study homogeneous nucleation and heterogeneous nucleation near defects. Notably, we discovered a surprising two-step nucleation behaviour during the s-s transformation between crystals with square and triangular lattices; during the process the system passed through an intermediate liquid stage (figure). This surprising phenomena can be expected to occur in crystals with constituents at any length scale, provided that solid–liquid interfacial energies are sufficiently small. Further, our single-particle experimental resolution enabled us to directly identify liquid nucleation precursors, which arise from particle-swapping loops rather than from defects, and to study the facets of evolving nuclei, whose energetics and growth rates exhibit rich phenomenology.
Buckling of Bilayer Films into Three-Dimensional Structures
 The elastic instabilities of thin two-dimensional (2D) sheets make possible new and promising strategies for building complex three-dimensional (3D) materials. In essence, a small film thickness renders out-of-plane buckling easier than in-plane stretching, because film-bending stiffness scales as thickness to the third power while film-stretching stiffness scales linearly with thickness. From an engineering perspective these instabilities can produce wrinkling, creasing, global buckling, and delamination. Often, such effects are not desirable for applications. However, inspired by paper folding techniques such as origami and kirigami, various groups have begun to develop new rules and material systems to harness mechanical instabilities and to create complex functional 3D morphologies from pre-designed structured thin films.
The elastic instabilities of thin two-dimensional (2D) sheets make possible new and promising strategies for building complex three-dimensional (3D) materials. In essence, a small film thickness renders out-of-plane buckling easier than in-plane stretching, because film-bending stiffness scales as thickness to the third power while film-stretching stiffness scales linearly with thickness. From an engineering perspective these instabilities can produce wrinkling, creasing, global buckling, and delamination. Often, such effects are not desirable for applications. However, inspired by paper folding techniques such as origami and kirigami, various groups have begun to develop new rules and material systems to harness mechanical instabilities and to create complex functional 3D morphologies from pre-designed structured thin films.
In our work, we employed surface topography as a new means to guide buckling of swollen polymer bilayer films and thereby control the morphology of resulting three-dimensional objects. Briefly, topographic patterns were created on poly(dimethylsiloxane) (PDMS) films which were then coated with a very thin layer of non-swelling parylene, i.e., coated on different sides of the patterned films. We then dipped the film into an organic solvent to induce swelling of the PDMS. After swelling in the organic solvent, the bilayer transformed into various structures, including half-pipes, helical tubules, and ribbons. We demonstrated these effects (figure) and introduced a simple geometric model that qualitatively captures the relationship between surface topography and swollen film morphology.
Glasses
Glassy materials are disordered like a liquid but resist mechanical stress like a solid. They have been used for thousands of years, yet many fundamental properties of these common household and industrial materials still remain unexplained. The so-called glass transition has been called one of the deepest mysteries in condensed matter physics, because it cannot be understood like other thermodynamic phase transitions such as crystallization. Investigations of glass transitions and structural arrest are also of broad interest because the new concepts thus generated affect understanding of a wide variety of materials across a wide swath of scientific communities, including molecular, colloidal, granular and polymeric ‘glasses’.
Phonons and the Boson Peak: Phonons, or vibrational modes, distinguish glasses from ordinary crystalline solids. Unlike crystals, for example, which are dominated by “sound” modes at low frequencies, disordered solids exhibit a so-called “boson peak” in the phonon density of states, wherein many more modes appear than expected for sound waves. The excess modes of the boson peak are believed to be responsible for the unusual behavior of the heat capacity and thermal conductivity at low-to-intermediate temperatures in glasses. We applied displacement correlation matrix techniques to our video microscopy particle tracking data in two-dimensional colloidal glasses to determine the phonon density of states and to visualize the phonon modes. The figure-left below shows a spectacularly clear observation of a boson peak in the phonon density of states (at frequency w*), which we found to grow in peak-height and shift to lower frequency/energy as the packing fraction decreased towards the melting point. The figure-right shows the quasi-localized nature of a typical vibrational mode for phonons in the boson peak (each point represents a particle, and the arrow shows amplitude and direction of its vibration).
In related measurements (see publications), we also measured the vibrational modes (phonons) and phonon dispersion relations in colloidal crystals, in colloidal glasses with and without attractive interactions, as well as in colloidal gels.
 Rearrangements, Phonons, and Soft Spots: Following up on our identification of these quasi-localized low frequency/energy phonon modes in glasses, we set out to test the hypothesis that these localized regions correspond to “soft spots” in glasses that are more likely to participate in rearrangements compared to other regions in the samples. We carried out experiments to identify soft spots (apparent from color scale in figure below), as well rearrangement regions (rearranging particles are circles in figure below) as a function of pressure on the glass. These experiments revealed spatial correlations between regions of high displacement in low frequency quasi-localized phonon modes (“soft spots”) and rearranging clusters of particles in the colloidal glasses. These results, which suggest a deep connection between rearrangement events and low-frequency vibrational modes in some glassy systems, offer new and quantitative ways to understand plastic deformation in disordered solids.
Rearrangements, Phonons, and Soft Spots: Following up on our identification of these quasi-localized low frequency/energy phonon modes in glasses, we set out to test the hypothesis that these localized regions correspond to “soft spots” in glasses that are more likely to participate in rearrangements compared to other regions in the samples. We carried out experiments to identify soft spots (apparent from color scale in figure below), as well rearrangement regions (rearranging particles are circles in figure below) as a function of pressure on the glass. These experiments revealed spatial correlations between regions of high displacement in low frequency quasi-localized phonon modes (“soft spots”) and rearranging clusters of particles in the colloidal glasses. These results, which suggest a deep connection between rearrangement events and low-frequency vibrational modes in some glassy systems, offer new and quantitative ways to understand plastic deformation in disordered solids.
Glasses with Repulsive versus Attractive Interactions: While much glass research focuses on identification of universal features, many properties of glasses depend on the details of the interparticle potentials of its constituents. Colloidal glasses with pure repulsive interactions between particles, for example, form when the packing fraction of the particles is made sufficiently large. However the addition of even a very small short-range attraction to interparticle potential in a repulsive glass can lead to the formation of so-called attractive glasses, which exhibit many new properties. Exploration of the similarities and differences between glasses composed of particles with attractive versus repulsive interactions holds promise for manipulating properties of glassy materials.
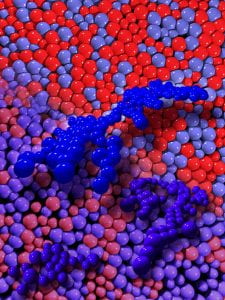
We have developed several different colloidal systems which offer us the ability to tune interparticle interactions. In one such system, based on temperature-tuning of a colloidal suspension in a binary-fluid background solvent, we created novel colloidal glasses whose interparticle potential could be tuned in situ from short-range repulsive (producing a repulsive glass) to short-range attractive (producing anattractive glass), while other parameters such as background suspension viscosity, particle packingfraction, and particle type are held constant. This capability enabled us to explore a recurring question in the glass community concerning the nature of the structural rearrangements that occur via the cooperativemotion of spatially clustered particles. These clusters are sometimes calledcooperative rearrangement regions (CRRs). We employed video microscopy to probe the dynamical and structural behaviors of the interaction-tunablecolloidal glasses with single-particle resolution. Among many effects, we discovered that the spatial shape of the typical cooperative rearrangement events were string-like structures in repulsive glasses but compact cluster-like structures in attractive glasses (see image above). The observations suggest that even though many properties are controlled by the short-range repulsive part of the interparticle potential, differences due to attraction at slightly longer range may have interesting consequences.
In related measurements (see publications), we also studied the glass vibrational modes (phonons) and the nature of individual particle displacements in glasses as a function of particle interaction.
Aging in Glasses: After initial formation, glasses relax via a nonequilibrium process called aging during which their dynamics slow dramatically and become more heterogeneous. How can glasses become more viscous and rigid over time without major changes to their structure? We created a unique experimental system to explore these and related questions. In particular, soft colloidal glasses were formed by suspending microgel spheres in water. The microgel particles are special in that their diameters vary with changes in temperature. Thus, using a lamp to focus light energy into the colloidal suspension, we are able to rapidly heat the spheres, causing them to shrink, move freely, and rearrange in an experimentally-induced liquid state. Then we remove the light, and thereby quench the entire system, returning the liquid to a glass state in about a tenth of a second. Thereafter, video microscopy is employed to follow the motions of all the colloidal atoms over time.
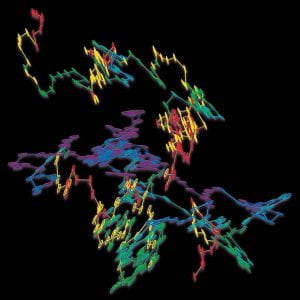
In studying aging, scientists have noticed that small clusters of particles tend to rearrange, even while the overall spatial distributions of particles remain roughly the same. Over time, it is believed that these clusters grow in size, making it more and more difficult for rearrangements to occur because such rearrangements require more and more cooperative motion. We studied these clusters over time during aging and discovered that one class of rearrangement event is particularly effective at bringing about the aging process. The number of these so-called irreversible rearrangement events decreased as the glass continued to age, and the number of particles required to move as part of these irreversible rearrangements increased as the glass aged. The figure to the right is a false color image derived from experiment that shows a cluster of fast moving particles associated with one such irreversible rearrangement event. Initially, such rearrangements of particles would occur in groups of 10 to 20. As time passed, and the glass continued to relax, an even more concerted effort was required to initiate an event. In this case, 50 to 100 particles moved to gain a better (energetically) particle configuration, slowing the process even further. The increase of irreversible rearrangement cluster size, as well as observation of an increase in number of stable particle configurations, directly leads to the slowing dynamics characteristic of aging. Additionally, we find that particles with local crystalline order are very unlikely to irreversibly rearrange. Thus a direct link between local crystalline order, particle rearrangement, and slowing dynamics is experimentally demonstrated.
Crystal-to-Glass Transition: Disorder plays a critical role in traditional melting andfreezing phenomena and in the formation of glasses. Melting from crystal to fluid, for example, is a sharptransition accompanied by loss of orientational and translationalorder and by a dramatic decrease in flow resistanceand rearrangement time scale. By contrast, orientationaland translational order are not changed significantlyat the liquid-to-glass transition, even as viscosity and rearrangementtime scale diverge. An interesting, less-studied but closely related problem concerns the role played by frustration and disorder in drivingthe transformation of a crystal to a glass. We have carried out experiments that probe this transition: from crystalline solid to glass as a function of quenched disorder. The experiments employ temperature-dependent nearly hard-sphere binary colloidal suspensions composed of two particle sizes with substantially different diameters. The number fraction of small diameter “dopant” particles is varied from 0.0 to 0.5, and the area fraction of the two-dimensional (2D) suspension is varied from 0.75 to 0.90 at each dopant concentration. This approach enables us to trace sample evolution as function of increasing quenched disorder at fixed area fraction. The resultant glassy phases acquire typical properties such as dynamic heterogeneity and disorder, but the crystal-to-glass transition is quite sharp, also exhibiting features often associated with melting.
Frustration (Colloidal Antiferromagnets)
Frustration is a feeling known to anyone who has had to choose one course of action from a range of imperfect options. Similar situations arise in nature, and scientific ideas about frustration have been explored to understand materials as varied as water, ceramics, magnets and superconductors. Geometric frustration in materials arises when the arrangement of constituents in space prevents simultaneous minimization of local interaction energies. A multiplicity of imperfect choices then leads to frustrated materials with many “lowest energy” states in which small perturbations can introduce giant fluctuations with peculiar dynamics.
The essence of the geometric frustration phenomenon is best captured in the model of magnetic (Ising) spins arranged on a two-dimensional (2D) triangular lattice and interacting anti-ferromagnetically. Two of the three spins on any triangular plaquette within this lattice can be anti-parallel to minimize their antiferromagnetic interaction energy, but the third spin is frustrated because it cannot be simultaneously anti-parallel to both neighboring spins (see schematic Figure). Such frustration leads to materials with extensive entropy proportional to the number of particles in the system. Traditionally, these phenomena have been explored in magnetism, wherein spins on each atom experience frustration as a result of their anti-ferromagnetic near-neighbor interactions and the lattice on which they sit. But it is difficult to observe individual spins directly. More recently, artificial arrays of mesoscopic constituents such as Josephson junctions, superconducting rings and ferromagnetic islands have been designed to study these phenomena, but observations have been limited to studies of static patterns.

Left: Schematic illustration of frustration between anti-ferromagnetically interacting spins at the corners of triangles. Right: Microscope image of frustrated colloidal anti-ferromagnet.
Recently, we developed a simple geometrically frustrated system composed of closely packed colloidal spheres confined between parallel walls (the figure shows a microscope image of the frustrated colloidal suspension). Packing frustration is created by arranging spherical particles in water on a flat triangular lattice, while permitting the particles to freely move small distances out of plane, that is, up or down, just a little bit. The frustrated material is formed because neighboring particles prefer to move away from one another. Thus, if a particle is in the down position, its neighbors will want to move to the up position. Since, the microspheres pack on the corners of each triangle, the lattice is geometrically frustrated. For every triangle, there is always at least one pair of energetically unfavorable neighbors that are both up or both down. These arrays of microgel spheres self-assembled into a buckled triangular lattice with either up (bright particles in image) or down (dark particles in image) displacements. Furthermore, the microgels are special; the microgel sphere particle diameter can be increased or decreased by varying sample temperature. Diameter tuning enables us to tune the strength of the effective anti-ferromagnetic interaction by changing sample temperature, and then to observe resulting effects at the ‘single spin’ level. The tunable soft-matter system thus provides a novel means to directly visualize the dynamics of frustration, thermal excitations and defects. Among other things, experiment and theory (by Lubensky & Shokev) reveal that single-particle dynamics are governed by in-plane lattice distortions that partially relieve frustration and produce ground states with zigzagging stripes and sub-extensive entropy, rather than the more random configurations and extensive entropy of the antiferromagnetic Ising model.
Since the experimental scenario emulates classic models of spin frustration, the research builds a novel connection between two very different fields of physics: soft matter and frustrated magnetism.
Brownian Motion
The study of Brownian motion and its generalizations has had a profound impact on physics, mathematics, chemistry, and biology. More than 100 years ago, Einstein described mathematically the random motion (Brownian motion) experienced by a small spherical particle suspended in a liquid. The particle moves because it is pushed around by the molecules in the liquid. The origin of this mysterious motion was explained in Einstein’s famous 1905 paper that established a relation between the diffusion coefficient of a Brownian particle and its friction coefficient.
Brownian Motion of Ellipsoids: One year after the famous 1905 paper, Einstein extended the concept of Brownian dynamics to rotational and other degrees of freedom. Particle anisotropy leads to dissipative coupling of translational to rotational motion and to physics first explored by F. Perrin. In recent experiments we have directly visualized the translational and rotational Brownian motion of ellipsoids, and in the process we have tested fundamental concepts about motions of anisotropic macromolecules.
We used digital video microscopy to study the Brownian motion of an isolated ellipsoid in suspension and in this way directly observed the coupling effects between rotational and translational motion. The experiments quantified the crossover from short-time anisotropic to longtime isotropic diffusion and directly measured probability distribution functions for the displacements. Taken together, the observations, numerical simulations, and interpretation with Langevin theory (with our theoretical colleague Tom Lubensky) provides insights into fundamental diffusive processes, which are potentially useful for understanding transport in membranes and for understanding the motions of anisotropic macromolecules. The Figure shows twenty seconds of a measured random walk trajectory for a micrometer-sized ellipsoid undergoing Brownian motion in water. The ellipsoid orientation, labeled with rainbow colors, illustrates the coupling of orientation and displacement and shows clearly that the ellipsoid diffuses faster along its long axis compared to its short axis.
In subsequent work we have explored how confinement between two walls affects ellipsoid diffusion anisotropy parallel and perpendicular to its central axis. These experiments test theories of hydrodynamic (fluid) drag in quasi-2D.
Other Brownian motion research (with spheres): We employed dynamic light scattering in the multiple scattering limit (i.e., the technique diffusing wave spectroscopy and its variants) to probe the Brownian motion of colloidal particles on the very shortest time scales, before the particle motions become purely diffusive (i.e., before particle mean-square displacements scale linearly in time). These experiments explored particle motion and hydrodynamic scaling on time scales of order the time it takes for fluid vorticity to travel one particle diameter. Related experiments measured the effects of particle concentration on the short-time diffusion coefficients of spheres in monodisperse and bidisperse colloidal suspensions, in the process testing many-body hydrodynamic theories of concentrated dispersions.
The Jamming Transition
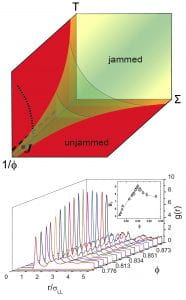
Schematic Jamming Phase Diagram and Maxima in the first peak of the particle pair correlation function close to the J-point.
Jamming is a physical process in which collections of objects (e.g., particles) are crammed together to behave as solids. The idea of jamming is that slow relaxations in many different systems, ranging from glass-forming liquids to suspensions of particles to foams and granular materials and even traffic jams, can be viewed in a common framework. For example, one can define jamming to occur when a system develops a yield stress or an extremely long stress relaxation time in a disordered state. Foams and granular materials flow when a large shear stress is applied but jam when the shear stress is lowered below a critical value. We have recently developed a colloidal system based on temperature-sensitive particles that permits study of the jamming point (i.e., the J-point). These microspheres swell and shrink by changing the temperature of the system and are small enough so that thermal motion is important. Thus, by increasing the diameter of these soft microspheres, we induce dynamic arrest or jamming in the suspension. Our investigation discovered (see Figure) a vestige, at non-zero temperature, of one of the important structural signatures to arise at the zero-temperature jamming transition. This observation of a maximum in the local particle structure at jamming suggests that molecules in a glass might retain an echo of the phenomenon of how boulders coming to rest to form a solid rock pile. Theory and computer simulation by Andrea Liu and Sid Nagel, combined with these novel experiments is providing new clues about the connections between jamming and the glass transition, as well as a concrete experimental route to explore these questions.
MELTING:
Premelting in Bulk Crystals

Slice through a three-dimensional colloidal crystal shows positions of ‘colloidal atoms’ and the onset of premelting at the grain boundary between two crystallites.
The importance of melting in nature can hardly be overestimated, and yet a detailed understanding of the mechanisms that drive this transformation is still evolving. Scientists have speculated for more than a century about how crystalline solids melt, in the process generating microscopic models emphasizing the role of lattice vibrations, dislocations, grain boundaries, surfaces, dimensionality, and combinations thereof. In contrast to the continuous transitions that arise in ferromagnetism and liquid-vapor systems, a first principle theory of the solid-liquid transition is difficult because of long-range many-body effects, symmetry, and a lack of universality. Furthermore, experimental investigations to test underlying theoretical assumptions are extraordinarily difficult, because they must track motions of individual atoms or defects within crystals. Nevertheless, recent experiments and theory have shown convincingly that atomic crystal surfaces, at equilibrium below the bulk melting point, often form melted layers. This premelting lowers the energy barrier for liquid nucleation and effectively prevents superheating of the solid.

Coexistance of solid and liquid in the colloidal crystal.
Theories have suggested a similar premelting occur at defects such as grain boundaries, stacking faults, and dislocations located within the bulk crystal, but these effects have not been observed. In recent work we imaged the motions of particles in three-dimensional colloidal crystals during the melting process. The images reveal premelting near grain boundaries and dislocations. Increased disorder is observed in crystalline regions bordering the defects as a function of defect type (e.g. grain boundaries, dislocations, vacancies), distance from the defect, and particle volume fraction.
These observations answer longstanding fundamental questions about melting mechanisms, suggest that grain boundary and dislocation premelting is an important effect in the melting process, and introduce new quantitative measures of local disorder. Besides their intrinsic importance for colloid science and technology, all indications suggest interfacial free energy is the crucial parameter for premelting. Thus these results are also relevant for atomic scale materials.
The colloidal crystals used for these studies are equilibrium systems composed of micron-size, nearly-hard-sphere particles. At high volume fraction these particles are driven entropically to condense into close-packed crystalline solids. A key feature of these measurements is our use of microgel particles, whose diameters depend on temperature. Thus by changing sample temperature slightly, we precisely vary the volume fraction of particles in the crystal over a significant range, driving the crystal from close-packing towards its melting point at lower volume fraction.
Melting of Layered Phases of Rods in Temperature Sensitive Polymer Solutions
Melting of three-dimensional (3D) crystals is among the most ubiquitous phase transitions in nature. In contrast to freezing, melting of 3D crystals usually has no associated energy barrier. Bulk melting is initiated at the crystal surface. We have recently investigated the pathways for melting of lamellar phases. In contrast to crystals which have 3D order, lamellar phases have one-dimensional (1D) quasi-long-range order. Additionally while 3D crystals have only one surface with coexisting gas or liquid, the lamellar phase is a microphase separated state in which the entire bulk is spanned by interfaces between immiscible materials. Lamellar structures are typically built from amphiphilic molecules such as surfactants, lipids and block copolymers, and their phase transformations provide insight about membrane biophysics. Although lamellar phases are frequently studied, melting transitions of lamellar into nematic phases are rarely observed. We have created a novel system that exhibits such melting, and we have shown this process is fundamentally different from melting of 3D crystalline solids.
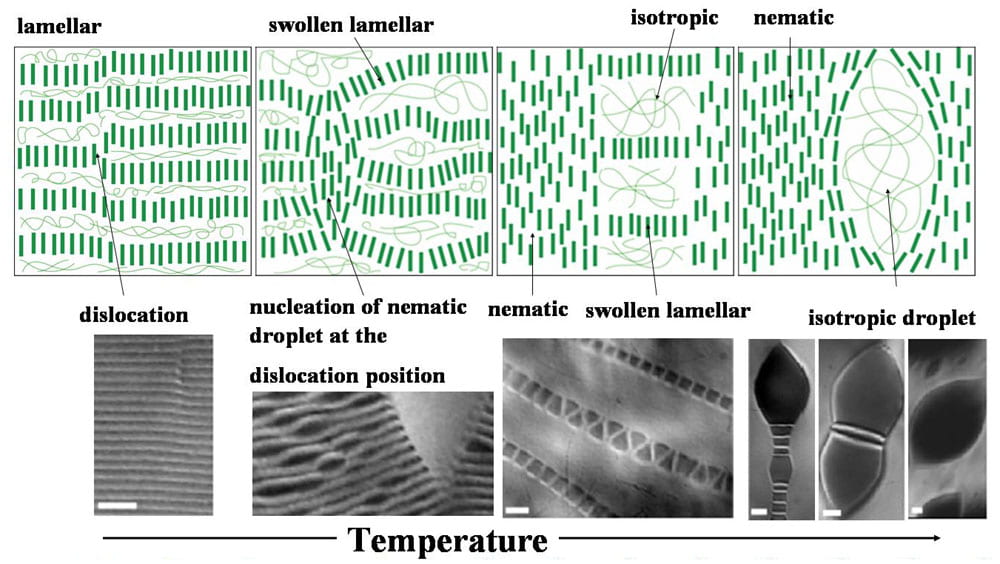
Lamellar, nematice and isotropic phases as a function of temperature in lyotropic rod-polymer solutions.
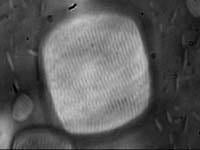
Melting of a lamellar droplet to a nematic droplet.
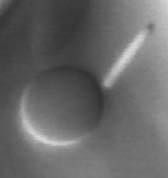
Melting of a single lamellae (one layer) of rods into a nematic droplet.
We have developed a temperature sensitive colloidal suspension to carry out these studies. The suspension is composed of lyotropic monodisperse rods of fd-virus, and thermosensitive Poly(N-isopropylacrylamide) (NIPA) polymer. The thermotropic character of the fd/NIPA mixture stems from the temperature dependent solubility of NIPA polymer in water. The resultant mixture forms isotropic, lamellar and nematic phases depending on temperature and constituent concentration. The temperature dependence of our system enables us to study previously inaccessible phase transition kinetics between lamellar phases and coexisting isotropic or nematic phases. We also observe droplets of smectic and nematic phases in an isotropic background, and single membranes of rods in an isotropic background. The sequence of phases observed in these temperature-sensitive rod-polymer suspensions is shown in the figure above. The mechanism for melting of these droplets and membranes can be studied in real time by optical microscopy.
Melting in Quasi-1D (Cylinders), 2D & Thin Crystalline Films Publications
Confinement and dimensionality profoundly affect crystal melting. In two-dimensions (2D), for example, melting sometimes proceeds in two-steps, from crystal to the so-called hexatic phase and then from hexatic to liquid phase. Such behavior is qualitatively different from well known one-step first-order bulk melting in three-dimensions (3D). Interesting related questions can be asked about thin crystalline films, which are not two-dimensional, nor fully bulk-like, and about ordered structures in quasi-1D. As such, melting behaviors and mechanisms present interesting fundamental questions and challenges for both theory and experiment. We have been exploring melting mechanisms of single- and poly-crystalline colloidal matter; colloids are outstanding thermodynamic model systems for melting studies, because the trajectories of all particles in the field-of-view are measurable by video microscopy with single-particle resolution, and because the inter-particle interactions are simple and well understood.

 In one recent investigation, for example, we created thin crystalline films confined between two glass walls. The films were composed of temperature-sensitive, diameter-tunable microgel spheres with short-ranged repulsive interactions. Using digital video microscopy, we observed their behavior during melting with single particle resolution for the first time. Among many observations, very thin solid films were found to abruptly melt into the liquid phase, while thicker films behaved more like conventional solids exhibiting traditional liquid-solid coexistence. A critical thickness of four layers marked the cross-over from one behavior to the other (the figure shows “rivers” of liquid forming within crystalline regions, whereas no such coexistence exists when there are fewer than five layers).
In one recent investigation, for example, we created thin crystalline films confined between two glass walls. The films were composed of temperature-sensitive, diameter-tunable microgel spheres with short-ranged repulsive interactions. Using digital video microscopy, we observed their behavior during melting with single particle resolution for the first time. Among many observations, very thin solid films were found to abruptly melt into the liquid phase, while thicker films behaved more like conventional solids exhibiting traditional liquid-solid coexistence. A critical thickness of four layers marked the cross-over from one behavior to the other (the figure shows “rivers” of liquid forming within crystalline regions, whereas no such coexistence exists when there are fewer than five layers).
In other recent investigations, we have observed solid-like phases of colloidal spheres packed into quasi-1D cylinders (see figure); the ordered phases exhibit long-range orientational order and melt into more disordered structures. We have also studied 2D melting using microgel spheres interacting via short-range repulsion, demonstrating the existence of the intermediate hexatic phase.
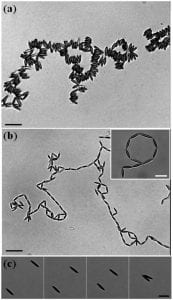
Top two panels show assembled chain-like structures formed by micron-size ellipsoidal particles at a water-oil interface. The chain morphology depends on the type of particle used. Bottom panel show two ellipsoids attracted to one another by capillary forces.
Capillary Interactions Between Anisotropic Colloidal Particles
The behavior of particle monolayers at fluid interfaces has attracted interest for many years and across many scientific communities. From a practical viewpoint, the stability of thin liquid films and interfaces in the presence of particles affects the control of a variety of materials including emulsions, foams, and coatings. On the basic science side, particle monolayers form beautiful model systems for studies of fundamental issues in condensed matter physics. Nevertheless, questions remain about the mechanism of particle interaction at a fluid interface and about how these interactions lead to formation of ordered and disordered structures. Perhaps the most important interparticle interaction arising at a fluid interface is due to lateral capillary forces. For heavy particles, these capillary interactions stem from the overlap of interface deformations brought about by gravity. Surprisingly, lateral capillary forces also arise for lighter, micron-sized particles. In this case, interfacial deformations can be of electric origin or can arise from irregular wetting at the particle surface.
Most experimental investigations of interparticle interactions and assembly at fluid-fluid interfaces have focused on spherical or nearly spherical particles. We have explored the behavior of anisotropic particles, ellipsoids, at the oil-water interface. Direct measurements of attractive capillary interactions between the ellipsoids are reported (bottom panel of figure). The interaction energies are very large compared to thermal energies and compared to the interaction energies of spherical particles with the same surface chemistry. In addition, the pair interaction potential exhibits a power law behavior, which suggests a description in terms of capillary quadrupoles. These anisotropic capillary forces lead to the assembly of open structures and chains rather than crystals or random aggregates (top two panels of figure).
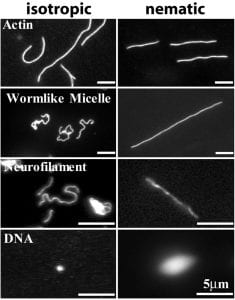
Biopolymers (fluorescently labeled) in suspensions of rods. The rods are fd-virus. The left column shows biopolymers in isotropic suspensions of rods, and the right column shows these same biopolymers in nematic suspensions of rods.
Biopolymers in Anistropic (Nematic) Fluids
Polymer coils in solution exhibit a variety of conformational and dynamical behaviors depending on many factors, including polymer concentration, polymer stiffness, solvent quality, solvent flow, and mechanical stress. We have explored the conformations of polymer coils in anisotropic solutions, in particular nematic solvents composed of aligned rod-like macromolecules. We show by direct visualization that semi-flexible biopolymers dissolved in the nematic phases assume an elongated rod-like configuration aligned with the background nematic director. The coil-rod transition depends on the persistence length (i.e. stiffness) of the biopolymer and the size of the rod-like macromolecules. Using theoretical models that incorporate polymer bending, polymer coupling to the background nematic director fluctuations, and nematic elasticity, we were able to quantitatively explore the fluctuations of these semi-flexible polymers and find they cannot be described by a theory which treats the nematic background as a fixed external field.
Mechanical Responses of Soft Materials: Macro- and Microrheology
The storage and dissipation of mechanical energy by soft materials is often surprisingly complex as a result of the hierarchical internal structure of these media. Elastic and viscous properties play an important role in the functioning soft material, and their precise origin is of fundamental interest. At PENN we are measuring these mechanical responses with conventional rheometry and with microrheology.
Relate links: Optical Imaging and Micromanipulation, Rheology Center
Microrheology has recently emerged as an important methodology for probing the viscoelastic properties of soft materials, providing access to miniscule sample volumes over a broader range of frequencies than conventional rheometry. In a typical microrheology experiment, the complex shear modulus of a material is derived by tracking the microscopic motions of tracer particles dispersed within the material. One-point microrheology is the traditional form of the microrheological measurement, wherein the mean-square displacements of single isolated particles are tracked. Two-point microrheology is based on measurement of the cross-correlated thermal motion of pairs of embedded tracer particles for determination of the complex shear modulus of the surrounding medium. By cross-correlating the thermal motion of pairs of embedded tracers, we isolate the motions resulting from wavelength undulations of the primary background complex fluid rather than the micro-scale inhomogeneities.
 In recent research we have used microrheology to explore the mechanical responses of thin layers that surround colloidal paricles in non-adsorbing semi-dilute polymer solutions of DNA (figure). Combining one-point (G1) and two-point (G2) microrheology with theory, we are able to assign a rheological size ( D ) to the thin layers surrounding the colloidal particles, by forcing the collapse of one-point data onto a single curve. The rheological layer was about twice as large as the polymer mesh size, indicating that there may exist a slip length between solvent and polymer that exceeds the polymer mesh size.
In recent research we have used microrheology to explore the mechanical responses of thin layers that surround colloidal paricles in non-adsorbing semi-dilute polymer solutions of DNA (figure). Combining one-point (G1) and two-point (G2) microrheology with theory, we are able to assign a rheological size ( D ) to the thin layers surrounding the colloidal particles, by forcing the collapse of one-point data onto a single curve. The rheological layer was about twice as large as the polymer mesh size, indicating that there may exist a slip length between solvent and polymer that exceeds the polymer mesh size.
Current research themes are oriented towards macroscopic rheometry of suspensions of sticky rods (e.g. carbon nanotubes), and mechanical responses and noise spectra in active systems (e.g. bacterial baths and gels).
Entropy-driven Colloidal Interactions and Self-Assembly (Background)
Entropic interactions are perhaps best understood in the context of suspensions of large- and small-diameter hard-spheres. Hard-sphere colloids lack attractive and long-range interactions, which typically compete with entropic effects to produce ordered phases. Nonetheless, as Asakura and Oosawa first noted in the 1950s, in mixtures of different size spherical particles an ordered arrangement of large spheres can increase the total entropy of the system by increasing the entropy of the small spheres. The basic idea underlying this phenomenon is depicted in Figure below. The box contains a few large spheres and many small spheres. The entropy of a small sphere depends on the number of positions it can occupy in the box, i.e. its free volume. More free volume means more entropy for the small spheres. Since the center of mass of the small sphere cannot penetrate within a/2 of the large sphere surface, a region of “excluded volume” surrounds each large sphere. Here, a(a L ) represents the small (large) sphere diameter. Thus, when the surfaces of the two large spheres approach within a small-sphere diameter, these excluded volume regions overlap one another, and the total volume accessible to the small spheres increases. The resulting increase in small sphere entropy induces the so-called attractive “depletion” or entropic force between the large spheres.
 Illustration of the entropic interactions of hard sphere particles among themselves and with the wall. The small sphere centers of mass are excluded from the shaded blue regions. The red regions correspond to the overlap of excluded volumes, and thus represent the gain in volume for the small spheres. Notice that the gain in volume near the surface is larger than that between two particles in the bulk. Note if figure is not colored, then blue = light grey and red = dark grey.
Illustration of the entropic interactions of hard sphere particles among themselves and with the wall. The small sphere centers of mass are excluded from the shaded blue regions. The red regions correspond to the overlap of excluded volumes, and thus represent the gain in volume for the small spheres. Notice that the gain in volume near the surface is larger than that between two particles in the bulk. Note if figure is not colored, then blue = light grey and red = dark grey.
Colloidal Interactions
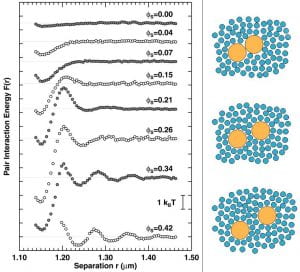
Potentials of mean force between two large colloidal spheres in a sea of small particles. Each curve represents a different background volume fraction of the small spheres. The data capture entropic (depletion) attractions at the smallest center-to-center separation, and oscillations due to the structural correlations of the ‘fluid’ of small spheres.
We have developed an experimental apparatus to directly measure particle interaction potentials in suspension. Using the instrument we have studied interaction potentials between colloidal particles brought about by added particles, non-adsorbing polymers, adsorbing polymers and rods. Our observations reveal information about colloid interactions, and about physics of the background medium such as its osmotic pressure and structure.
Related links: Light Forces, Center for Advanced Imaging and Micromanipulation
An example of directly measured entropic potentials is shown in the figure to the right. The experimental sample consisted of suspensions of large and small hard spheres. We probe the interactions between two large spheres as a result of a sea of small spheres. The most prominent feature in these potentials is the entropic attraction at short range. The liquid structure of the smaller particles in the background becomes important when their concentration is increased. Even at relatively low small-sphere volume fractions, there is a substantial entropic repulsion at separations of order one small sphere diameter from contact. Simple models do not predict this repulsion. Qualitatively the effect arises because the small spheres tend to form in layers around the large spheres. When the gap between the large spheres is commensurate with these layers, the free energy is lower; when the gap is incommensurate, the energy is higher.
Self-Assembly of Colloidal Particles (Entropy-driven & Beyond)
The entropic excluded volume effects that induce attractions between particles, induce even stronger attractions between particles and walls. For example, in our lab we have demonstrated that these attractions between particles lead to crystallization and phase-separation in mixtures of particles of different sizes, particles and polymers, etc. We are using similar effects to position particles on substrates or move them in a predetermined ways. In particular, we have shown that geometric features on a surface can create entropic force fields that trap, repel, or induce drift of the larger particles in suspension. Large particles, moving in the vicinity of steps, grooves, or corners cut into a flat substrate, modify the small-sphere free volume in a manner dependent on large particle position and on the size and shape of the geometric features (see below figure for schematic examples). We have identified and quantified these phenomena at step edges, near corners, and in vesicles.
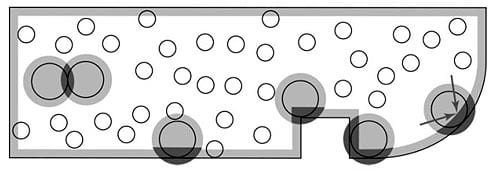
Schematic of the entropic ‘depletion’ effect in various geometries. Dark shaded region represents the gain of small sphere excluded volume (entropy).
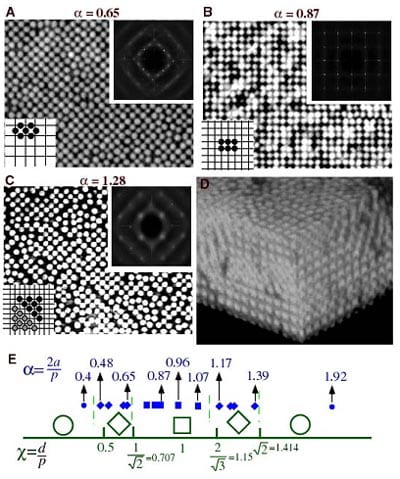
Colloidal assembly on cross-grating templates. Images show PMMA spheres. For all data the volume fraction of the PMMA particles is 0.25, and the concentration of polystyrene polymer is 0.1 mg/ml. In (E) we show the sequence of two-dimensional structures that nucleate on the grating template at particular ratios of the mean interparticle spacing, d, to the grating spatial period, p. The structures in (A), (B) and (C) are commensurate with the template. (D) is a 3D confocal image showing 20 layers of an FCC crystal.
Building on this concept, we devised arrays of such structures in order to self-assemble particles in a chosen pattern, thus introducing a qualitatively new approach to colloidal epitaxy based on equilibrium thermodynamics and geometry. We used templated surfaces with spatially periodic 1-dimensional (1D) and 2-dimensional (2D) height profiles to create a periodic surface potential, and then to drive the growth of two- and three-dimensional (3D) particle structures nucleating from these templates. Some of the self-assembly effects we saw on these templates are shown in figure right.
Current research explores self-assembly in microgravity, self-assembly of non-spherical particles on surfaces and in the bulk, convective assembly of particles on templated surfaces, and colloidal crystal templates filled with liquid crystalline material.
CARBON NANOTUBES
Isolated single-wall carbon nanotubes exhibit large electrical and thermal conductivities, extraordinary mechanical strength and rich optical spectra. Carbon nanotube complex fluids provide a diversity of new phenomenology in suspension, and are potentially of enormous technological utility. We have applied concepts and methods from soft condensed matter to control single-wall carbon nanotubes (SWNTs) in solution. Our initial research discovered a class of surfactants that stabilized SWNTs in aqueous suspensions extraordinarily well. This first observation led us to pursue several, initially unanticipated questions in nanotube science and application. Some of this work will be described below.
The Yodh lab has worked on a variety of scientific problems in this field. Selected recent research is described below.
Solubilization of Single-Wall Carbon Nanotubes in Aqueous Suspensions

Left-to-Right are single-wall carbon nanotube suspensions in water stabilized by surfactants SDS, Triton-X and NaDDBS respectively.
Many envisioned applications employing the unique electronic, thermal, optical and mechanical properties of SWNTs require large-scale manipulation of stable suspensions at high weight-fraction. Tube solubilization provides access to solution-phase separation methodologies, facilitates chemical derivatization, controlled dispersion and deposition, microfluidics, fabrication of nanotube-based fibers and composites, and optical diagnostics. A barrier for these applications has been the substantial van der Waals attractions between tubes which causes aggregation.
We developed a methodology for creation of high weight-fraction suspensions of surfactant stabilized SWNTs in water, with a large fraction of single tubes. Our methodology is essentially a single step solubilization scheme, in which nanotubes are mixed with surfactants in low-power high-frequency sonicators for long time periods; the scheme enhanced disaggregation of bundles with dramatically reduced tube breakage. The critical ingredient was the surfactant sodium dodecylbenzene sulfonate (NaDDBS), consisting of a benzene ring moiety, a charged group, and an alkyl chain. Appropriate deployment of NaDDBS enhanced the stability of SWNTs in water by factors of tens to hundreds compared to commonly employed surfactants and polymers. New and quantitative insight about nanotube solubilization was derived from comparisons of single tube yield, measured by AFM, as a function of surfactant type, and concentration.
Current research uses these nanotube complex fluids as starting materials for deposition onto substrates for electrical devices, and for creation of mechanically strong composites.
Nematic Nanotube Gels

Filaments (single-wall carbon nanotubes) are dispersed in a polymer gel, which is subsequently compressed to a fraction of its original size. The condensed gel creates a macroscopic aligned (nematic) phase, interesting topological defects, and potentially novel mechanical responses.
Many of the interesting properties of single-wall carbon nanotubes are anisotropic due to the large length-to-diameter ratio of carbon nanotubes; responses measured parallel to the nanotube central axis differ from those measured in other directions. Thus many of the potential applications of SWNTs aim to produce composite materials with aligned nanotubes in order to take full advantage of these anisotropic responses. A nematic phase of SWNTs, similar to those of thermotropic and lyotropic liquid crystals, offers a natural route for creation of aligned composites.
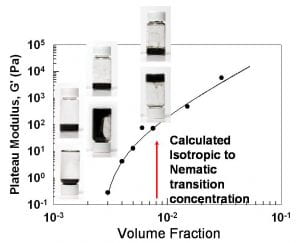
To this end, we have created nematic nanotube gels. The gels contain large domains of oriented SWNTs that exhibit hallmark properties of a nematic: birefringence, anisotropy in optical absorption, and liquid crystalline defects. We created these nematic nanotube gels by embedding isolated surfactant coated nanotubes in a crosslinked gel at low density, and then inducing a volume phase transition (compression) of the gel by changing its temperature. Apparently the gel network prevented the close contact between parallel nanotubes that produces bundling, and compression produced mass densities of isolated nanotubes, not accessible in simple aqueous suspensions, that favor their alignment. In addition to the potential importance of this approach for nanotube technology, these lyotropic gels represent a new physical system different from both lyotropic hard-rod suspensions and from thermotropic elastomers, with which they share the property of nematic order in a randomly crosslinked gel. They exhibit an interesting interplay between local nematic alignment and local mechanical stresses and cracks. Finally, the general methodology we have introduced for making these materials provides a qualitatively new way to induce phase transitions in soft materials such as colloids, emulsions, and other complex fluids.
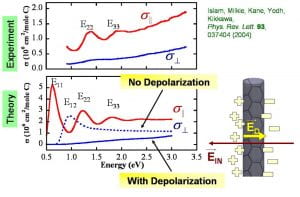
Measured optical absorption cross-sections parallel and perpendicular to the carbon nanotube long axis as a function of photon energy. The lower panel shows theory (Kane, PENN) for these effects with and without field depolarization effects.
Optical Properties and Anistropy of Single-wall Carbon Nanotubes
The substantial length-to-diameter aspect ratio of SWNTs presents a fundamental structural anisotropy that influences optical absorption. In a recent experiment we (in close collaboration with the Kikkawa group at PENN) have obtained the polarized absorbance cross-sections of single-wall carbon nanotubes. To achieve this goal we weakly aligned surfactant (NaDDBS) stabilized SWNT suspensions in a magnetic field and subsequently locked them in place by suspension gelation using NIPA polymer. Polarized Raman scattering was then used to determine the nematic order parameter (i.e. SWNT alignment) for each sample. This alignment information was combined with polarization-sensitive absorbance data to recover the absolute wavelength-dependent SWNT absorption cross-section for light polarized parallel and perpendicular to the nanotube central axis. These data enabled us to rigorously test theories for absorptive processes, and provided the first direct confirmation that sub-band features are absent from the cross-polarized channel, as theoretically predicted. Moreover, these anisotropic spectra facilitate simple, rapid, and quantitative measurements of nanotube orientations in bulk dispersions and composites.
Current research (also with the Kikkawa group) is focussed on magnetic alignment and alignment anisotropies.
Rigidity percolation of NaDDBS/Carbon-nanotube suspensions as a function of nanotube volume fraction.
Structure and Rheology of Single-wall Carbon Nanotube Suspensions
The mechanical properties of associating semi-flexible polymer and rod networks play a critical role in a variety of materials’ contexts ranging from functioning cells to stress-bearing colloidal suspensions and polymeric composites. Generally the rheology of these networks depends on many factors including the bonds between rods, rod concentration, and rod flexibility. The relationship, however, between the microscopic structure and the macroscopic elasticity of associating networks of stiff rods remains essentially unexplored. We have investigated the viscoelastic properties of an associating rigid rod network: aqueous suspensions of surfactant stabilized single wall carbon nanotubes (SWNTs). The SWNT suspensions represent a fascinating model system, enabling us to isolate the contributions of bonding to the macroscopic elasticity of rod networks. Our experimental observations suggest nanotubes in suspension form an interconnected network with bonds that freely rotate and resist stretching. Suspension elasticity originates from bonds between nanotubes rather than from the stiffness or stretching of individual nanotubes. The suspensions exhibit rigidity percolation as a function of nanotube concentration. Our experiments provide new rheological understanding about solutions of carbon nanotubes. This new information may improve our ability to control the processing precursors of these novel composites.
We have also carried out small-angle neutron scattering (SANS) to probe the structure of these nanotube suspensions. The investigation provides strong evidence for individual SWNTs and very small bundles in suspension which behave like rigid rods. A crossover in the power law Q-dependence of scattered intensity, suggests that these isolated tubes and small bundles also form a loose three-dimensional network.
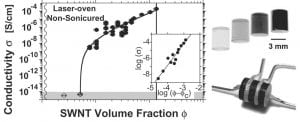
Top right – Single-wall nanotube carbon nanotube composites as a function of nanotube concentration (black is most concentrated). Bottom right – Configuration for 4-probe electrical conductivity measurements. Left – Electrical percolation as a function of nanotube volume fraction.
Single wall carbon nanotube epoxy composites
We (with Kikkawa group) have developed procedures to introduce single wall carbon nanotubes (SWNTs) into thermoset epoxies . We have characterized the morphology of the systems, and then explored the electrical conductivity of the resulting composites as a function of SWNT length, SWNT concentration, sample homogeneity, and sample preparation. We observe sharp (percolation-like) conductivity onsets, at very low SWNT concentrations. These lower thresholds result from our new synthetic methods, and by minimally altering mechanical properties of the epoxy may pave the way for important technological applications such as electrostatic charge dissipation, RF shielding, etc.
Current experiments (with Kikkawa group) probe thermal transport in similar composites, deducing interfacial thermal resistances.
Hard Surfaces & Interfaces
The goals of these programs are to understand interfaces and their role in modifying the microscopic properties of adjoining bulk materials & adsorbed molecules. The Yodh lab has worked on a variety of scientific problems in this field. Selected recent research is described below.
Nonlinear Optical Spectroscopy of Interfaces, Surfaces and Particles
Our group uses nonlinear optics (e.g. second-harmonic and sum-frequency generation) to probe level structure, charge dynamics, and defects at solid-solid interfaces. The experiments combine the intrinsic interface sensitivity of three-wave mixing processes with the long penetration depth of light to make possible a range of studies of buried solid-state interfaces. Such materials are very difficult to probe with conventional tools from surface science and linear optics. Scientific contributions include the discovery of intrinsic quantum well interface states at the ZnSe/GaAs interface and midgap defect states in Au/GaAs junctions. Nonlinear spectroscopy was also combined with photomodulation techniques to elucidate morphological properties associated with interface traps, trap lifetimes, strain and strain relaxation. More recently we have explored second-harmonic generation from colloidal particles, and we have been developing and using nonlinear microscopy for studies of complex media, including brain.
Ultrafast Spectroscopy of Surfaces and Surface Adsorbates
A second family of measurements employed ultrafast infrared methodologies to study vibrational dynamics of molecules on metal surfaces in ultrahigh vacuum. The objectives of this program were to resolve very fast processes such as energy transfer, dephasing, and the movement of adsorbed molecules, particularly following ultrafast laser excitation of the substrate. For example, we measured the energy transfer rate from metal substrate electrons and phonons to the very low frequency vibrations (i.e. the frustrated translation mode) of a chemisorbed diatomic molecule, following femtosecond visible light pulse excitation of the substrate.
Soft Materials & Complex Fluids
Coffee Ring Physics
Liquid Crystal Physics
Solid-Solid Phase Transitions
Topography Guided Buckling
Glasses
Frustration (Colloidal Antiferromagnets)
Brownian Motion
The Jamming Transition
Melting:
Premelting in Bulk Crystals
Melting of Layered Phases of Rods in Temperature Sensitive Polymer
Melting in Quasi-1D (Cylinders), 2D & Thin Crystalline Films
Capillary Interactions Between Anisotropic Colloidal Particles
Biopolymers in Anistropic (Nematic) Fluids
Mechanical Responses of Soft Materials:
Macro- and Micro-rheology
Entropy-driven Colloidal Interactions and Self-Assembly (Background)
Colloidal Interactions
Self-Assembly of Colloidal Particles (Entropy-driven & Beyond)
Solubilization of Single-Wall Carbon Nanotubes in Aqueous Suspensions
Nematic Nanotube Gels
Optical Properties and Anistropy of Single-wall Carbon Nanotubes
Structure and Rheology of Single-wall Carbon Nanotube Suspensions
Single wall carbon nanotube epoxy composites
Nonlinear Optical Spectroscopy of Interfaces, Surfaces and Particles
Ultrafast Spectroscopy of Surfaces and Surface Adsorbates